21.02.2022-26.02.2022
Тема: Створення
та відтворення графічнихоб’єктів
Теоретична частина
Практична частина
Завдання
1. Перевірити роботу гарячих клавіш в середовищі MS Word
Alt+Й -
перехід до поля "Скажіть, що потрібно зробити";
Ctrl+O – відкриття
нового об’єкта;
Ctrl+S – збереження
виділеного об’єкта;
Ctrl+W – закриття
виділеного об’єкта;
Ctrl+X – вирізання
виділеного об’єкта;
Ctrl+С -
копіювання виділеного об’єкта;
Ctrl+V
- вставлення виділеного об’єкта;
Ctrl+A –
вибрати(виділити) всі об’єкти;
Ctrl+B - виділення
жирним відмічених об’єктів;
Ctrl+I - виділення
курсивом відмічених об’єктів;
Ctrl+U -
підкреслення відмічених об’єктів;
Ctrl +
"[" - зменшення розміру шрифту на 1 пункт;
Ctrl + "]" -
збільшення розміру шрифту на 1 пункт;
Ctrl+E -вирівнювання
тексту по центру;
Ctrl+L -вирівнювання
тексту за лівим краєм;
Ctrl+R - вирівнювання
тексту за правим краєм;
Esc –
скасування активної дії відкритого об’єкта;
Ctrl+Z -
скасування результату виконаної останньої дії;
Ctrl+Y - повторення
скасованої дії.
Ctrl+H –замінити символи на
інші;
Ctrl+S – зберегти текстовий
документ в файлы,
Ctrl+N –створити новий
документ
Завдання
2.
Робота з об’єктами в текстовому процесорі MS Word
Знайти інструменти на стрічці
інструментів в MS Word, щоб:
1)змінити
назву шрифту(гарнітура) у тексті «Крутий
учень» на: а)Franklin Gothic Medium;
б) Monotype Corsiva; в) Arial Black; г) Calibri. Зберегти файл з виконаним завданням.
2)змінити
розмір шрифту у тексті «Кмітлива
учениця» на а) 22 пт; б) 26,5 пт; в) 40,5 пт.
3)змінити
накреслення шрифту(Ж; К; П) у
тексті «Слава Україні!» на підкреслений курсив.
4)налаштувати
ефекти у тексті «Героям слава!»та налаштувати 3D – об’ємну гарнітуру
шрифту.
5)налаштувати
колір виділення тла тексту «Україна – це ми!» на а)фіолетовий; б) жовтий.
6) змінити
на надрядковий індекс усі парні символи у тексті «Школа-ліцей»; Зберегти файл.
7)змінити на
підрядковий індекс усі непарні символи у тексті «Форматування»;
8)видозмінити
текст «Зошит для редагування» на основі вами створеного нового стилю;
9) змінити
текст «Вітер, дощ, сніг, туман» на список маркований з трьома різними
маркерами;
10) змінити
текст «Вітер, дощ, сніг, туман» список нумерований. Зберегти файл.
11)налаштувати
спеціальний відступ ліворуч 1-го рядка абзацу ліворуч за допомогою
маркерів на горизонтальній лінійці на
1,5 см. Зберегти файл.
12) змінити
пропуск між символами у словосполученні «Чарівні слова» на 5 пт;
13)підняти усі парні символи у слові «Вітчизна» на 5
пт вгору і налаштувати до слова довільні текстові ефекти(світіння, тінь, 3D). Зберегти
файл.
14) опустити
усі непарні символи у слові «Батьківщина» на 5 пт вниз і налаштувати до
слова текстові ефекти(світіння, тінь, 3D). Зберегти файл.
15)відформатувати
словосполучення «Вінниця – перлина Поділля» як заголовок 1 рівня;
16)відформатувати
словосполучення «Фонтани Вінниці» як заголовок 2 рівня;
17)відформатувати
один абзац у три стовпці з жовтою
заливкою та блакитними межами; 18)встановити міжрядковий інтервал у абзаці 2
пт. Зберегти файл.
20)розірвати
чотири сторінки і створити закладки на кожній сторінці; змінити розмір парних
сторінок на формат А3 альбомної орієнтації, змінити непарних сторінок на формат
А5.
21)
налаштувати межі сторінок та водяний
знак на сторінках у вигляді тексту «ліцей 7»; 22)налаштувати вирівнювання
абзацу по ширині;
23)змінити
стиль абзацу стиль «Строгий» та застосувати рівень контуру 3;
24)виокремити
цитату у тексті власним стилем
«Святковий»;
25)із
трьох заголовків та трьох підзаголовок сформувати автоматичний зміст;
26)
сформувати на сторінці таблицю розміром 3х8 і і залити в ній перший рядок
блакитним кольором;
27)
сформувати на сторінці таблицю розміром 3х8 і і залити в ній перший рядок
блакитним кольором;
28) створити
фігуру трикутник і залити його довільним
зображенням стильно оформити
межі і і написати на трикутнику текст червоного кольору «Трикутне зображення»;
29) накласти
два різних зображення та змінити прозорість першого зображення на сторінці;
30) у
таблицю 2х2 записати формули периметру та площі прямокутника;
31) створити
титульну сторінку для підручника з математики;
32)створити
три порожні сторінки і вставити нижній та верхній колонтитули з текстовими
написами сьогоднішньої дати, номером сторінки;
33)створити
порожню таблицю 4х100 на двох сторінках і створити розрив таблиці на другу
сторінок; 34)форматувати стильно автофігуру трапеція і на ній написати слово
«Трапеція»;
35) створити
схему на сторінці про ваш шлях від школи
до дому;
36)створити
накладання різних фігури і згрупувати їхні, змінити у цих фігур плани(задній
план на передній план);
37) створити
схему розташування парт та меблів у класі;
38)створити
на трьох сторінках три гіперпосилання з
однієї сторінки на іншу;
39)за
допомогою закладок створити кнопкову навігацію на трьох сторінках;
40) на
чотирьох сторінках створити перехресне гіперпосилання, а саме: зі ст1 на ст3,
та зі ст2 на ст4;
41)у верхній
колонтитул поставити як зображення текст «Ліцей №7»;
42)у нижній
колонтитул поставити таблицю 2х2 без меж;
43) вставити
номер сторінки на середину правого поля;
44) у
текстове поле помістити Гімн України і розташувати його точно в центрі сторінки;
45)Створити
виноску у тексті на одне слово «Інформатика», у виносці записати тлумачення
цього слова.
46) створити
переноси слів у тексті на інший рядок;
47) зберегти
як форматі шаблон документа та запам’ятати його розширення;
48) зберегти
документ у формат PDF відкрити цей документ у форматі PDF;
49)
встановити на документ пароль і зберегти його, відкрити цей документ
використовуючи пароль.
50)
прочитати метадані збереженого текстового документа та переглянути його в
режимі структура.
Завдання 3. Створити
об’ємні фігури в MS Word
1. Для об’єкту авто фігура -
трикутник: створити цей об’єкт, знайшовши відповідний інструмент в
текстовому процесорі MS Word. Гарячими
клавішами скопіювати і вставити три рази цей об’єкт.
2. Для цих трьох об’єктів змінити їхні
параметри(текстура-заливка, контур, прозорість) та налаштувати інші значення
параметрів()(права кнопка мишки, Формат рисунка)
3. Для цих трьох об’єктів знайти вкладку
інтерфейсу MS програми, в якій розміщено інструменти для зміни 2D на 3D параметри і налаштувати об’ємні фігури.
4. Згрупувати ці об’єкти за
критеріями: 1)об’єкти, що містять в собі символ; 2)об’єкти, що не
містять в собі символи; 3) об’єкти, які не відповідають критеріям 2
та 1.
Результати виконаної практичної частини
надіслати на електронну адресу: vinnser@gmail.com
************************
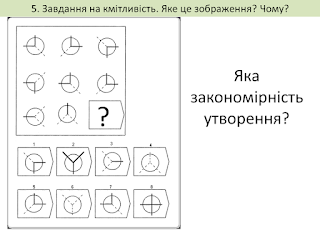
Завдання на розвиток кмітливості
Завдання 1.
Означення. Будь-яке число, яке можна
подати, як суму двох однакових натуральних чисел, називають парним.
Парні числа позначають формулою m = 2n.
Парних
чисел безліч.
Парні
числа, закінчуються на цифри: 0, 2, 4, 6, 8.
Приклади. Такі числа є парними: 2,
4, 6, 8, 56, 78, 40.
Означення. Будь-яке число, яке не
можна подати, як суму двох однакових натуральних чисел, називають непарним.
Непарні
числа позначають формулою m = 2n - 1.
Приклади. Такі числа є непарними:
21, 43, 65, 87, 56, 781, 409.
Непарних
чисел безліч.
Непарні
числа, закінчуються на цифри: 1, 3, 5, 7, 9.
Варто звернути увагу на те, що сума парної кількості непарних чисел є
парною.
Узагальнення
цього факту виглядає так:
парність
суми кількох чисел залежить лише від парності числа непарних доданків:
якщо
кількість непарних доданків є (не)парна, то і сума також є (не)парною.
Це
можна зрозуміти з таких властивостей парності:
2∙n + 2∙k + … + 2∙f + 2∙q = 2∙(n + k + … +
f + q) = 2∙m
СУМА БУДЬ-ЯКОЇ КІЛЬКОСТІ ПАРНИХ ЧИСЕЛ ЗАВЖДИ ПАРНА.
2∙n
– 2∙k – … – 2∙f – 2∙q = 2∙(n – k – … – f
– q) = 2∙m
РІЗНИЦЯ БУДЬ-ЯКОЇ КІЛЬКОСТІ ПАРНИХ ЧИСЕЛ ЗАВЖДИ ПАРНА.
(2∙n -1)+ (2∙k-1)+ … + (2∙f-1) + (2∙q-1) =
2∙(n + k + … + f + q)- 2s = 2∙(m-s)
СУМА ПАРНОЇ КІЛЬКОСТІ НЕПАРНИХ ЧИСЕЛ ЗАВЖДИ ПАРНА.
(2∙n -1)+ (2∙k-1)+ … + (2∙f-1) + (2∙q-1) =
2∙(n + k + … + f + q)- 2s -1 = 2∙(m-s) -
1
СУМА НЕПАРНОЇ КІЛЬКОСТІ НЕПАРНИХ ЧИСЕЛ ЗАВЖДИ НЕПАРНА.
Таким чином,
парність результату не залежить від розстановки плюсів і мінусів між цілими числами,
а залежить тільки від кількості непарних чисел
в початковому наборі. Зрозуміло, що сума будь-якої кількості парних чисел є
завжди парним числом.
Звертаємо увагу ще на одну цікаву властивість.
Сума квадратів парної
кількості непарних чисел є парною.
(2∙n -1)2
+ (2∙k-1)2 + … + (2∙f-1)2 + (2∙q-1)2
= 2∙p
(парна кількість непарних доданків)
Сума квадратів непарної
кількості непарних чисел є парною.
(2∙n -1)2
+ (2∙k-1)2 + … + (2∙f-1)2 + (2∙q-1)2
= 2∙p – 1
(непарна кількість непарних доданків)
Зокрема,
сума двох
квадратів натуральних чисел може при
ділені на 4 мати остачу 0, 1, 2, але не
може мати остачу 3.
Приклади: 12 + 22 = 4 + 1,
12 + 32 = 4∙2 + 2,
22 + 22 = 4∙2 + 0.
Варто
запам’ятати, що n2 + k2 ¹ 4∙m + 3.
Узагальнення
попередніх фактів виглядає так:
Парність
суми довільних натуральних степенів кількох чисел залежить лише від
парності числа непарних доданків:
якщо
кількість непарних доданків є (не)парна, то і сума також є (не)парною.
Це
можна зрозуміти з таких властивостей парності:
(2∙n)z
+ (2∙k)n + … + (2∙f )s + (2∙q)t
= 2∙p
(будь-яка кількість доданків)
СУМА cтепенів БУДЬ-ЯКОЇ КІЛЬКОСТІ ПАРНИХ ЧИСЕЛ ЗАВЖДИ ПАРНА.
(2∙n)z - (2∙k)n - … -
(2∙f )s - (2∙q)t = 2∙p
(будь-яка кількість
доданків)
РІЗНИЦЯ cтепенів БУДЬ-ЯКОЇ КІЛЬКОСТІ ПАРНИХ ЧИСЕЛ ЗАВЖДИ ПАРНА.
(2∙n -1)z
+ (2∙k-1)n + … + (2∙f-1)m
+ (2∙q-1)w = 2∙p
(парна кількість непарних
доданків)
СУМА cтепенів ПАРНОЇ КІЛЬКОСТІ НЕПАРНИХ ЧИСЕЛ ЗАВЖДИ ПАРНА.
(2∙n -1)z
+ (2∙k-1)n + … + (2∙f-1)m
+ (2∙q-1)w = 2∙p - 1
(непарна кількість непарних доданків)
СУМА cтепенів НЕПАРНОЇ КІЛЬКОСТІ НЕПАРНИХ ЧИСЕЛ ЗАВЖДИ НЕПАРНА.
Звертаємо увагу ще на одну цікаву і не зовсім очевидну властивість.
Степінь
натурального числа (більша першої степені) не може бути записана у вигляді 4m +
2. Варто запам’ятати,
що nk ¹ 4∙m + 2, де натуральне k більше 1.
Зокрема,
можна довести такі властивості.
Довільна
степінь
непарного числа вигляду 4∙q +1 подається у вигляді 4∙p + 1:
(4∙q + 1)n = 4∙p + 1.
Або
цю рівність можна розуміти ще отак: будь-яка степінь непарного числа вигляду 4∙q +1
при діленні на 4 дає остачу 1.
Приклади:
(4∙2 +1)2 = 4∙20 + 1, (4∙2
+1)3 = 4∙182 +1, (4∙2 +1)4
= 4∙1640 +1.
Непарна степінь непарного числа вигляду
4∙q + 3 подається у вигляді 4∙p + 3:
(4∙q + 3 )2n-1 = 4∙p + 3.
Або
цю рівність можна розуміти ще отак: будь-яка непарна степінь непарного числа
вигляду 4∙q +3 при діленні на 4 дає остачу 3.
Приклади:
(4∙2 +3)3 = 4∙332 + 3.
Парна степінь непарного числа вигляду
4∙q + 3 подається у вигляді 4∙p + 1:
(4∙q + 3 )2n = 4∙p + 1.
Або
цю рівність можна розуміти ще отак: будь-яка парна степінь непарного числа
вигляду 4∙q +3 при діленні на 4 дає остачу 1.
Приклади:
(4∙2 + 3)2 = 4∙30 + 1, (4∙2
+3)4 = 14640 +1.
Задачі на дослідження парності чисел:
Задача
1. Петро купив загальний зошит на 96 аркушів і пронумерував всі його сторінки
по порядку числами від 1 до 192. Василь вирвав з цього зошита 35 аркушів і
додав всі 70 чисел, що на них були написані. Чи міг він дістати 1990?
Відповідь: ні, не могло. Вказівка. На кожному аркуші сума номерів
сторінок непарна, а сума 35 непарних чисел
є непарна.
Задача
2. Добуток 22 цілих чисел дорівнює 1. Доведіть, що їх сума не дорівнює нулю.
Вказівка.
Серед цих чисел – парне число "мінус одиниць", а для того, щоб сума
дорівнювала нулю, їх має бути рівно 11.
Задача
3. Чи можна скласти магічний квадрат з перших 36 простих чисел?
Відповідь:
ні, не можна. Серед цих чисел одне (це 2) – парне, а інші непарні. Тому в
рядку, де стоїть двійка, сума чисел непарна, а в інших – парна.
Задача
4. В ряд записано числа від 1 до 10. Чи можна розставити між ними знаки
"+" та "–" так, щоб значення отриманого виразу дорівнювало
нулю?
Відповідь:
ні, не можна. І справді, сума чисел від 1 до 10 дорівнює 55, і змінюючи в неї
знаки, ми змінюємо весь вираз на парне число.
Зауваження. Врахуйте, що від'ємні числа також бувають парними та
непарними.
Задача
5. Коник-стрибунець стрибає вздовж прямої, причому першого разу він стрибнув на
Вказівка.
Доводиться так само, як і в задачі 20, бо сума 1 + 2 + … + 1985 непарна.
Задача
6. На дошці виписано числа 1, 2, 3, ..., 1984, 1985. Дозволяється стерти з дошки
будь-які два числа і замість них записати модуль їх різниці. Врешті-решт на
дошці залишається одне число. Чи може воно дорівнювати нулю?
Відповідь:
ні, не може. Перевірте, що при зазначених операціях парність суми всіх
написаних на дошці чисел не змінюється.
Тепер
пропонуємо на ваш розгляд більш складні задачі, розв'язання яких, крім
парності, використовує, як правило, і деякі додаткові міркування.
Задача
7. Чи можна покрити шахматну дошку доміношками розміром 1x2 так, щоб вільними
залишились тільки клітинки а1 і, h8?
Відповідь:
не можна. Кожна доміношка покриває одне чорне і одне біле поле, а при викиданні
полів а1 і h8 чорних полів залишається на 2 менше, ніж білих.
Задача
8. До 17-цифрового числа додали число, яке записано тими ж цифрами, але в зворотному
порядку. Доведіть, що хоча б одна цифра суми, що отримана, є парною.
Вказівка.
Розгляньте два випадки: сума першої і останньої цифр числа менша 10, і сума
першої і останньої цифр числа не менш 10. Якщо припустити, що всі цифри суми
непарні, то в першому випадку не може бути жодного переносу в розрядах (що,
очевидно, приводить до суперечності), а в другому випадку наявність переносу
при русі справа наліво або зліва направо чергується з відсутністю переносу,
внаслідок чого ми одержимо, що цифра суми в дев'ятому розряді обов'язково
парна.

















Немає коментарів:
Дописати коментар